Enhancing archival datasets with machine learned psychometrics
Today I was reading a paper advocating the idea that science is slowing down because we have changed to incentivizing boring stuff that gets cited a lot instead of potentially far-reaching ideas that may not work out. Feeling bold because of this, I want to put out a radical idea.
What if we could improve the scoring of traits in archival datasets where the subjects are either dead, or not available for re-testing? This might have large implications for GWASs which often rely on large databanks with poorly measured phenotypes. The general idea that geneticists are using is combining related traits in genomic SEM, or MTAG. However, we can do much better.
In our ISIR 2019 presentation (Machine learning psychometrics: Improved cognitive ability validity from supervised training on item level data), we showed that one can use machine learning on cognitive data to improve the predictive validity of it. The effect sizes can be quite large, e.g. one could predict educational attainment in the Vietnam Experience Study (VES) sample (n = 4.5k US army recruits) at R2=32.3% with ridge regression vs. 17.7% with IRT. Prediction is more than g, after all. What if we had a dataset of 185 diverse items, and we train the model to predict IRT-based g from the full set, but using only a limited set using the LASSO? How many items do we need when optimally weighted? Turns out that with 42 items, one can get a test that correlates at .96 with the full g. That's an abbreviation of nearly 80%!
Now comes the fancy part. What if we have archival datasets with only a few cognitive items (e.g. datasets with MMSE items) or maybe even no items. Can we improve things here? Maybe! If the dataset has a lot of other items, we may be able to train an machine learning (ML) model that predict g quite well from them, even if they seem unrelated. Every item has some variance overlap with g however small (crud factor), it is only a question of having a good enough algorithm and enough data to exploit this covariance. For instance, I have found that if one uses the 556 items in the MMPI in the VES to predict the very well measured g based on all the cognitive data (18 tests), how well can one do? I was surprised to learn that one can do extremely well:
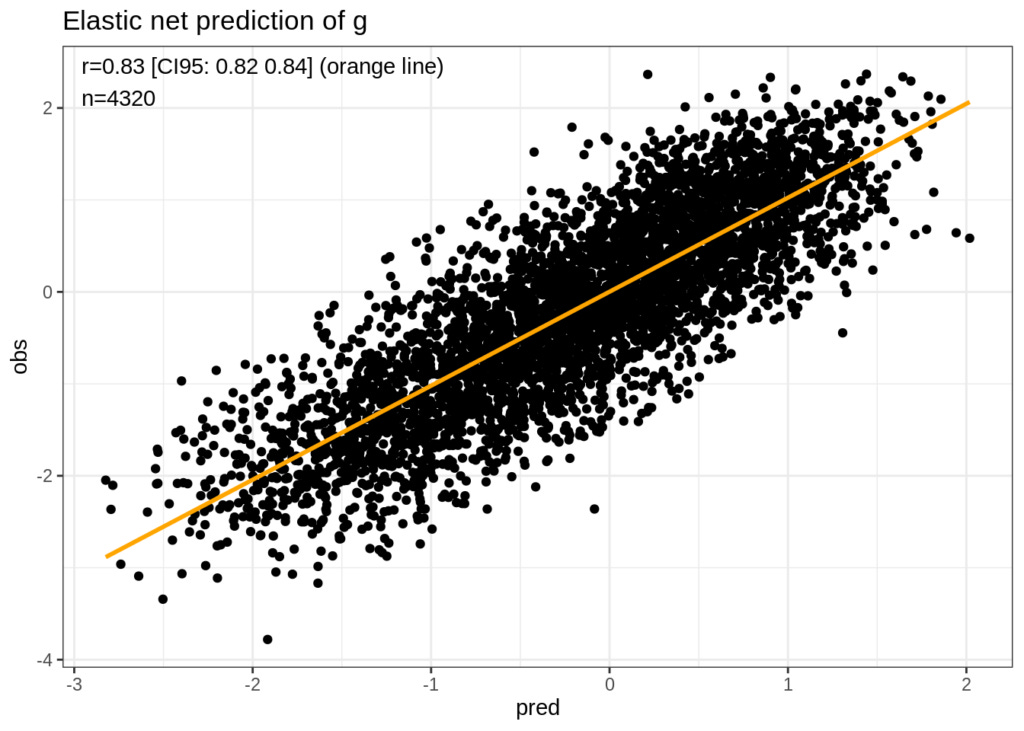
Thus, one can measure g as well as one could with a decent test like Wonderlic, or Raven's without having any cognitive data at all! The big question here is whether these models generalize well. If one can train a model to predict g from MMPI items in dataset 1, and then apply it to dataset 2 without much loss of accuracy, this means that one could impute g in potentially thousands of old archival datasets that include the same MMPI items, or a subset of them.
The same idea applies to training on cognitive items. Consider the widely used General Social Survey (GSS). It has a pretty poor 10 item vocabulary test, which may correlate .70ish with a fullscale IQ (no one knows!). However, what if we had a dataset where we have the same 10 vocabulary items along with a big dataset of other cognitive items. Then we could extract a good g from the full set of items (e.g. 200 items), and then train a ML model to predict g from the 10 Wordsum items. I bet it will work a lot better than using IRT. Unfortunately, no one seems to have used the Wordsum items with any other such set of items, except for the original data collection in the 1940s! So, what we need is for someone to simply collect this data. I suggest that we compile a set of public domain items from ICAR and other databases, and then administer them to some large samples (at least a few thousand people, but preferably 10k+). With this data, one can train the ML model and see whether I am right by predicting the good g in the GSS and seeing whether this has larger correlates with criterion variables such as income, education, and anything else that g relates to (this increased accuracy cannot be from overfitting because we did not train the model on GSS data). If this is feasible, it means we can now enhance measures of g in basically any dataset we can find as long as it has a bunch of items we can find in another dataset with good cognitive data.
Naturally, this kind of approach would generalize to any other trait you can think of. Potentially, it could result in a general improvement of scales available in all kinds of social science datasets, leading to improved outcomes for GWASs, and other models.
If you think this sounds like an exciting idea and want to fund it, get in contact. I expect this initial data collection would cost 2-3k USD, and we would of course publicly release this data.

