How many human genomes do we need for accurate genetic prediction models?

Back of the envelope and simple simulations

In a recent thread on X, I added:

Why do we need so much genetic data? Well, there are 3B positions in the genome, about 1% of them vary (30M). To fit an accurate regression model with them, need about 100 cases per predictor, so ~3B humans, or ~40% of ALL humans alive today.

Let's unpack this.

The human genome has about 3 billion base pairs (bp), that is, locations (loci). Most of these loci have no variation, all humans have the same letters there. These are therefore irrelevant for prediction models.

About 1% of the loci has some appreciable level of variation, thus about 30 million loci. Many of these are very rare, say occur in less than 0.1% of humans ('rare variants').

Finally, these variants all have to go into a prediction model to predict the outcome. The simplest and best case scenario is that our outcome is a normally distributed variable (like height almost is) and that all the variants linearly and additivelv combine. In other words, all we have to do is estimate a single parameter (trait change as function of an increase in minor allele count) for the 30M variants. In other words, nature has specified a true value for these 30M parameters and we just have to estimate these correctly, so we can use the model for perfect predictions insofar as genetics is concerned.

So how many genomes (subjects, cases) do we need to estimate such a model? There are a variety of recommendations:

Green [5] used statistical power analysis to compare the performance of different rules-of-thumb for how many subjects were required for linear regression analysis. These rules-of-thumb can be classified into two different classes. The first class consists of those rules-of-thumb that specify a fixed sample size, regardless of the number of predictor variables in the regression model, whereas the second class consists of rules-of-thumb that incorporate the number of SPV. In the former class, Green described a rule, attributable to Marks, that specifies a minimum of 200 subjects for any regression analysis. In the latter class, Green described a rule, attributable to Tabachnick and Fidell, who suggested (with what Green described as some hesitancy) that although 20 SPV would be preferable, the minimum required SPV should be five. Another rule attributed to Harris is that the number of subjects should exceed the sum of 50 and the number of predictor variables. Schmidt [6] determined that, in a variety of settings, the minimum number of SPV lies in the range of 15 to 20. In a similar vein, Harrell [2] suggested that 10 SPV was the minimum required sample size for linear regression models to ensure accurate prediction in subsequent subjects.

So authors don't agree, but perhaps 5 to 20 in this best case scenario. Thus, under these recommendations we would need about 30M * 5-20, that is, 150M-600M subjects in our study. Right now, if we pooled all available datasets we could maybe achieve 10M. Pooling them in practice is impossible due to data restrictions (e.g. 23andme won't give you a copy of their 3M+ customers' data), so maybe the largest one could achieve right now is pooling the largest datasets (UKBB 500k, AOU 250k, Danish 370k, JBB 200k and so on). Maybe a research team could get to 2M subjects.

However, things are considerably worse in reality because:

1. Most genomes are not deep whole genome sequencing (WGS), but array data with only 600-900k variants measured. The rest must be imputed with error.

2. Many outcomes are not normally distributed, but low frequency dichotomous outcomes (e.g. pancreas cancer).

3. The true model is not just additive and linear, but nonlinear (having 2 copies of an allele is not twice the effect of having 1 copy, dominance), or interactive (variants depend on the effects of other variants, epistasis, GxG), and in the worst case, may involve interactions with environmental variables so one would have to include these and their interactions (GxE).

4. The heritability of the trait is not necessarily high, and lower heritability models are harder to estimate (more noise).

5. The genetic variants are not normally distributed, but are count variables with possible values of 0, 1, or 2. I am not sure how this affects things.

6. The genetic variants are highly correlated locally. If you have TT at position 1, then the adjacent variant at position 100 is usually very highly correlated with this (linkage disequilibrium, LD). These high correlations may it difficult for the model to figure out which variant is doing what.

We are making good progress on (1) as major datasets are coming out with WGS data (e.g. UKBB). This problem will be mostly gone in the next 10 years.

There isn't anything we can do about (2), but this results in a much larger required dataset. In a typical recommendation in the literature for logistic regression, 10 events per variable is suggested, thus if we have a rare outcome with 1% frequency in humans, we would need not 300M genomes, but 300M with that outcome, so in total 30B cases. This is more than the number of humans that exist (8B). We would need to collect data for multiple generations and increase fertility rates to achieve this sample size.

Concerning (3), recommendations for complex models that allow for these kinds of effects are a lot more data hungry than linear regression, and can easily require 50 cases per variable or more. If the outcome variable is also binary and rare, then this pushes the amount of data we need beyond human capability.

Concerning (4 and 6), we can estimate heritabilities of traits and see how this affects conclusions.

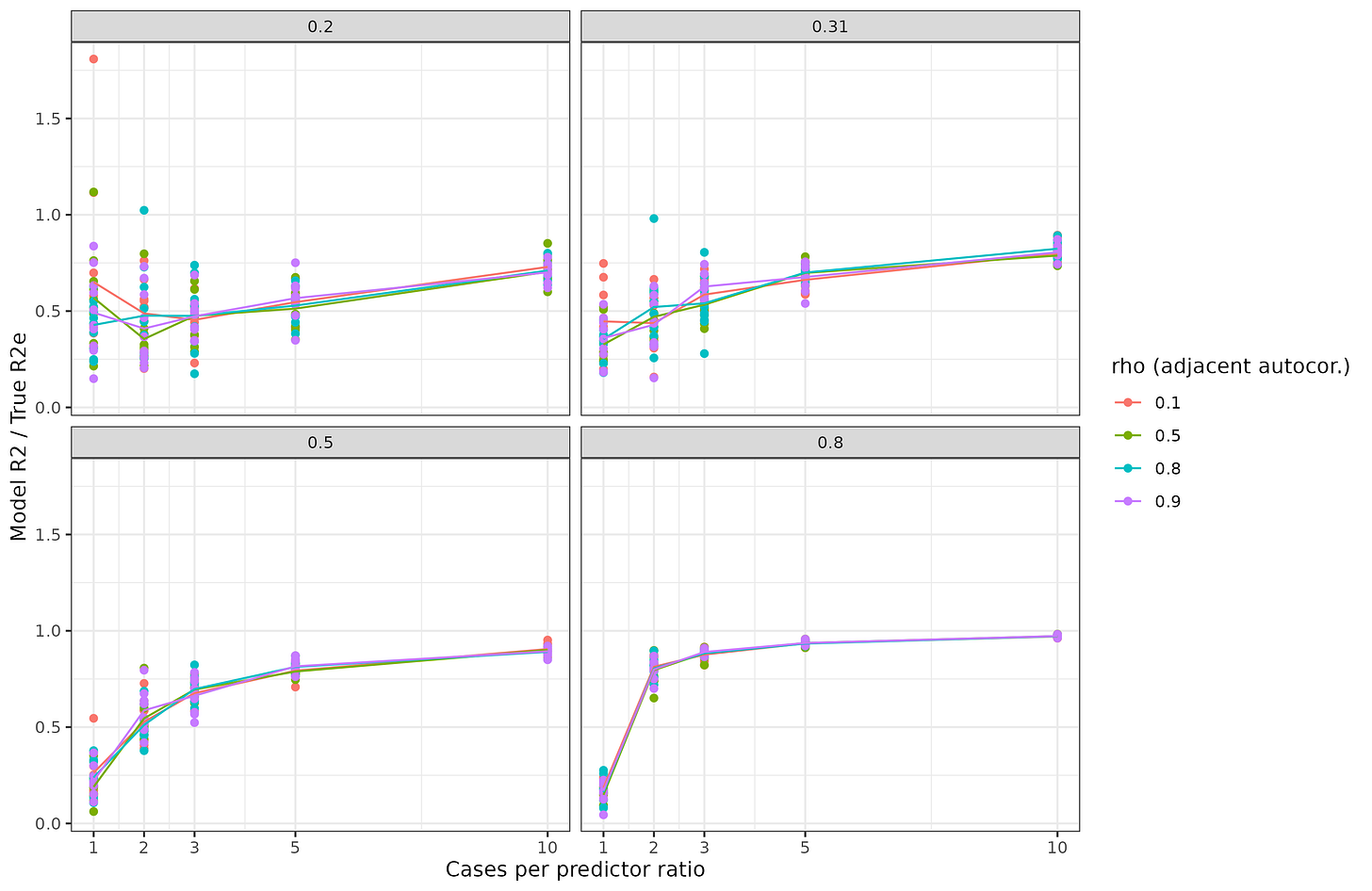
To illustrate and verify some of the above, I carried out a small simulation study. I simulated 100 multivariate normal variables with an autocorrelation (AR1) structure with a given strength (rho). Then I converted them to [0-2] count variables to be allele count-like. Then I assigned them random betas and made the outcome variable, which is thus normally distributed. Finally, I added some noise to this and built a linear model to predict it. I estimated the true validity of such models using cross-validation. Results:

The X axis has the number of cases per predictor. Since there are 100 predictors, the sample size ranged from 100 to 1000. The amount of autocorrelation between adjacent genetic variants was varied between 0.1 and 0.9. Thus, if the rho is 0.9, loci 1 and 2 correlate at 0.9, and loci 1 and 3 correlate at 0.9² = 0.81, and so on. Thus, it looks like this:

The actual correlations will be somewhat weaker because count variables result in weaker correlations.

Back to the results above, the Y shows the cross-validated model r2 divided by the true model r2, thus 1 is a perfect recovery of the true model insofar as predictions are concerned. The values on the facets (grey bars) are the heritabilities, that is, the maximum possible genetic prediction accuracy in r2 value. Thus, in the bottom right plot, we see that training a model with 100 cases and 100 predictors, for a highly predictable outcome does not result in a great model, we recover about 30% of the validity. This corresponds to the case of training with 30M subjects. If instead one has a sample of 500 (ratio 5), most of the model accuracy is recovered, 95% or so. For a less heritable trait, 20% in the top left, we see that even if we have 10 subjects per predictor (300M subjects), we can still only recover about 70% of the validity.

Thus, the simulations bear out our expectations in general. The numbers would be worse if we also made the outcome binary and so on. When I wrote my tweet about needing 100 genomes per genetic variant, this was my guesstimate for adjusting for the various difficulties I noted above. No one really knows how many genomes we will need, but certainly a very large number. A further issue is that due to data sharing regulations, researchers do not fit regression models with all their genetic variants, they fit them one at a time (singular regression, or what we call GWAS), and then try to combine them afterwards in a way that avoids overcounting (usually some variant of clumping). This introduces certain ineffieciencies as well. As such, I don't think my initial estimate is so far off. In our best case scenario, height:

This latest GWAS of height (Yengo et al. Citation2022) is the first of what is referred to as a “saturation” GWAS. Such a GWAS is so highly powered that further increases in the sample size without increases in participant diversity or variant inclusion are unlikely to reveal any additional genetic insights. In this landmark study conducted in 5.4 million individuals, the largest sample ever assembled for a GWAS, Yengo et al. identified an unprecedented 12,111 independent signals associated with height clustered into 7,209 non-overlapping loci that are enriched near genes with known Mendelian effects on skeletal growth. Together these loci comprise 21% of the genome, a result consistent with previous estimates (Shi et al. Citation2016). The results are notable not only because of their potential use in the discovery of novel height-modifying genes but also because they showed for the first time near exhaustion of GWAS’s ability to discover further associations, particularly in European ancestry populations. Such an outcome had been previously hypothesised to be possible but never actually demonstrated (Visscher et al. Citation2017; Kim et al. Citation2017; Wray et al. Citation2018).

we have reached a sample size of 5.4M, and we reached an accuracy of:

40-45% of variance. Given that height has a heritability of 80-95%, we recovered 42-56% of the full r2. Although to be precise, for prediction purposes, r2 is the wrong metric to use (and so are ratios of r2's), we have attained a model that predicts with about r = 0.65, versus a perfect model of r = 0.95, thus we have attained about 70% of the maximum validity already. This is the best case scenario: a politically uncontroversial trait which is normally distributed, easy to measure accurately, and with a very high heritability. For traits without one or more of these good properties, we will need larger samples in the order of 100s of millions to billions. We will get there! Denmark has already collected genomes from 6% of the population (370k/6M).