National chess skill: European culture, intelligence
http://www.unz.com/jthompson/chisalas-last-word/
How far should the net be cast as regards intellectual achievements? I suggest as far and wide as possible, or it will be assumed that some results are being held back. I favour those achievements which are in a “universal language” like maths, science and chess. There will always be some doubt about whether people in poor countries have access to knowledge and training, though the spread of internet access goes a long way to dealing with this. (In fact, it should level the playing field in terms of access to knowledge). Poker, Bridge, Backgammon, and Mahjong could be added to the list, because there are international competitions and rankings. I am not suggesting anyone should take part in such activities. Live and let live.
Chess a universal language like math? Methinks not. I took a quantitative look at FIDE players. Using data science tricks, I obtained a list of top 5k players and their countries. Then I did some plotting and modeling. Details can be found at http://rpubs.com/EmilOWK/chess_top5k_fide
Per capita rate ~ IQ

Obviously there are issues with country size, so we can weigh cases by sqrt(population) as we usually do.
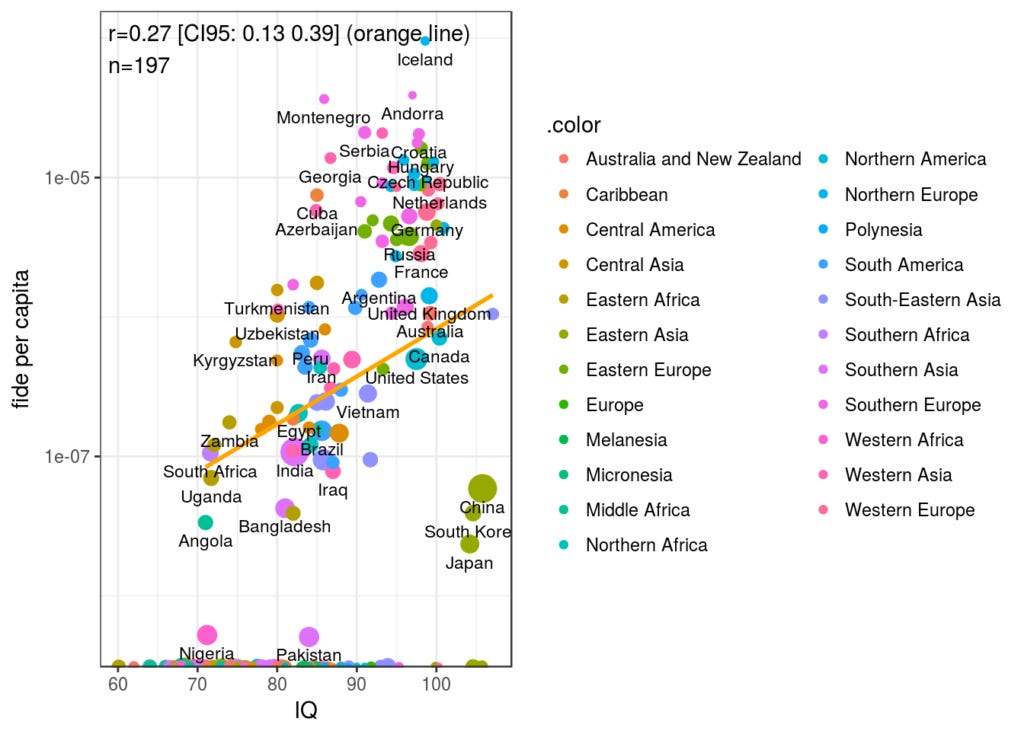
Did not help. It is obvious that East Asian countries are outliers, and that we have issues with a large number of countries with no top chess players at all. If we use the log count approach that Noah used in the terrorism papers, which seems superior to the per capita approach (though the reason for this is unclear to me, somehow handles sampling error better), then a simple model finds a strongish effect of IQ:
Linear Regression Model
rms::ols(formula = log_count ~ log_pop + IQ, data = natdata)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 197 LR chi2 140.48 R2 0.510
sigma0.5491 d.f. 2 R2 adj 0.505
d.f. 194 Pr(> chi2) 0.0000 g 0.636
Residuals
Min 1Q Median 3Q Max
-1.68341 -0.31570 -0.01964 0.39061 1.28864
Coef S.E. t Pr(>|t|)
Intercept -4.9833 0.4018 -12.40 <0.0001
log_pop 0.3281 0.0416 7.88 <0.0001
IQ 0.0405 0.0036 11.21 <0.0001
Note that these are unstandardized coefficients, and thus not easy to compare. Neither is the effect size easy to understand since the outcome is a log10 count. The model output says that for 1 IQ increase, the expected number of log10(count + 1) FIDE champions increase by 0.04. So, if I'm not mistaken, this translates into 10^.04. The scaling is not linear. The model predicted number of FIDE players for countries with IQ 70, 80, ..., 110 are 0.15, 1.93, 6.45, 17.93, 47.11. Or a factor of ~300 going from Africa level IQ to good cities.
However, most of this is due to the confound with European culture. If we add continent dummies, we get:
Linear Regression Model
rms::ols(formula = log_count ~ log_pop + IQ + UN_continent, data = natdata)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 197 LR chi2 219.72 R2 0.672
sigma0.4537 d.f. 6 R2 adj 0.662
d.f. 190 Pr(> chi2) 0.0000 g 0.730
Residuals
Min 1Q Median 3Q Max
-1.22161 -0.24685 -0.01719 0.25710 1.34260
Coef S.E. t Pr(>|t|)
Intercept -2.7309 0.4861 -5.62 <0.0001
log_pop 0.4035 0.0392 10.28 <0.0001
IQ 0.0164 0.0048 3.44 0.0007
UN_continent=Africa -1.1256 0.1464 -7.69 <0.0001
UN_continent=Americas -0.6569 0.1191 -5.52 <0.0001
UN_continent=Asia -0.9505 0.1044 -9.10 <0.0001
UN_continent=Oceania -0.7782 0.1512 -5.15 <0.0001
The IQ coefficient declines substantially. If we imagine possible European countries with IQs from 70 to 110, they are expected to have 13, 19, 28, 41, 60 top 5k persons, or factor ~4.6, down from ~300 before. 4.6 is still quite a few, of course. Empirically, this model predicts that reality should work like this:

Whereas, if we plot the IQs and counts with slopes by continent, they look like this:

Notice the lack of a noticeable slope for Asia, mainly due to the Singapore, Japan, Koreas (but not China). So, we are probably grouping some countries that shouldn't. We can also use UN's provided smaller regions, though these are arguably too small. We get (setting Western Europe as the comparison):
Linear Regression Model
rms::ols(formula = log_count ~ log_pop + IQ + UN_region, data = natdata)
Model Likelihood Discrimination
Ratio Test Indexes
Obs 197 LR chi2 267.20 R2 0.742
sigma0.4227 d.f. 24 R2 adj 0.706
d.f. 172 Pr(> chi2) 0.0000 g 0.767
Residuals
Min 1Q Median 3Q Max
-1.08552 -0.22309 -0.01046 0.22147 1.15614
Coef S.E. t Pr(>|t|)
Intercept -4.3280 0.7710 -5.61 <0.0001
log_pop 0.4198 0.0408 10.30 <0.0001
IQ 0.0316 0.0072 4.37 <0.0001
UN_region=Australia and New Zealand -0.6845 0.3344 -2.05 0.0422
UN_region=Caribbean -0.2719 0.2528 -1.08 0.2836
UN_region=Central America -0.6612 0.2456 -2.69 0.0078
UN_region=Central Asia -0.1106 0.2775 -0.40 0.6907
UN_region=Eastern Africa -0.8351 0.2534 -3.30 0.0012
UN_region=Eastern Asia -1.5121 0.2154 -7.02 <0.0001
UN_region=Eastern Europe 0.1641 0.2029 0.81 0.4198
UN_region=Europe -1.1183 0.4521 -2.47 0.0143
UN_region=Melanesia -0.8061 0.2655 -3.04 0.0028
UN_region=Micronesia -0.3599 0.2910 -1.24 0.2179
UN_region=Middle Africa -0.6288 0.3038 -2.07 0.0400
UN_region=Northern Africa -0.7298 0.2578 -2.83 0.0052
UN_region=Northern America -0.4391 0.2610 -1.68 0.0943
UN_region=Northern Europe 0.0283 0.2008 0.14 0.8882
UN_region=Polynesia -0.4774 0.3069 -1.56 0.1216
UN_region=South America -0.4197 0.2131 -1.97 0.0505
UN_region=South-Eastern Asia -0.9609 0.2065 -4.65 <0.0001
UN_region=Southern Africa -0.5514 0.3087 -1.79 0.0758
UN_region=Southern Asia -0.8013 0.2472 -3.24 0.0014
UN_region=Southern Europe 0.0403 0.1946 0.21 0.8362
UN_region=Western Africa -0.7804 0.2805 -2.78 0.0060
UN_region=Western Asia -0.5917 0.2050 -2.89 0.0044
Now IQ's beta went back up again (0.0316).
What if we use the per capita approach?
Linear Regression Model
rms::ols(formula = fide_per_million ~ IQ, data = natdata, weights = sqrt(population2017))
Model Likelihood Discrimination
Ratio Test Indexes
Obs 197 LR chi2 14.86 R2 0.073
sigma264.0903 d.f. 1 R2 adj 0.068
d.f. 195 Pr(> chi2) 0.0001 g 1.280
Residuals
Min 1Q Median 3Q Max
-3.4973 -1.2864 -0.4563 0.4652 92.7449
Coef S.E. t Pr(>|t|)
Intercept -7.3254 2.2682 -3.23 0.0015
IQ 0.1024 0.0262 3.91 0.0001
I changed the outcome to top players per million, otherwise all the coefficients were tiny. We see a coefficient of 0.10 here, meaning that 1 IQ point increases the per million player by 0.10. If we use the usual model predictions (for 70, ..., 110), this gives us values of -0.16, 0.87, 1.89, 2.91, 3.94. Negative values are of course impossible, but this model isn't constrained to disallow such values (could be done with e.g. Bayesian priors). The violation isn't too great anyway. If we add the small regions:
Linear Regression Model
rms::ols(formula = fide_per_million ~ IQ + UN_region, data = natdata,
weights = sqrt(population2017))
Model Likelihood Discrimination
Ratio Test Indexes
Obs 197 LR chi2 77.29 R2 0.325
sigma239.2931 d.f. 23 R2 adj 0.235
d.f. 173 Pr(> chi2) 0.0000 g 2.709
Residuals
Min 1Q Median 3Q Max
-7.70820 -0.62140 -0.03586 0.31916 87.33090
Coef S.E. t Pr(>|t|)
Intercept -5.5729 8.0336 -0.69 0.4888
IQ 0.1117 0.0800 1.40 0.1647
UN_region=Australia and New Zealand -4.4978 3.1416 -1.43 0.1540
UN_region=Caribbean -1.4467 2.8945 -0.50 0.6178
UN_region=Central America -3.5594 2.3098 -1.54 0.1251
UN_region=Central Asia -2.3240 2.6887 -0.86 0.3886
UN_region=Eastern Africa -2.4938 2.6692 -0.93 0.3515
UN_region=Eastern Asia -6.0083 1.6921 -3.55 0.0005
UN_region=Eastern Europe 0.4284 1.7746 0.24 0.8095
UN_region=Europe -4.6798 7.4075 -0.63 0.5284
UN_region=Melanesia -3.7884 3.6618 -1.03 0.3023
UN_region=Micronesia -3.7728 7.3435 -0.51 0.6081
UN_region=Middle Africa -1.9938 3.1464 -0.63 0.5271
UN_region=Northern Africa -3.4613 2.2871 -1.51 0.1320
UN_region=Northern America -4.8395 2.0390 -2.37 0.0187
UN_region=Northern Europe 2.7450 2.0215 1.36 0.1762
UN_region=Polynesia -4.1905 8.1261 -0.52 0.6067
UN_region=South America -3.4319 1.9566 -1.75 0.0812
UN_region=South-Eastern Asia -4.2342 1.8029 -2.35 0.0200
UN_region=Southern Africa -2.3886 3.2924 -0.73 0.4691
UN_region=Southern Asia -3.4515 2.0883 -1.65 0.1002
UN_region=Southern Europe 2.6375 1.9077 1.38 0.1686
UN_region=Western Africa -2.2252 2.8600 -0.78 0.4376
UN_region=Western Asia -1.8373 1.9890 -0.92 0.3569
The beta of IQ remained about the same, but it now has p = .16. There is too much noise to reliably see the signal. This can also be seen in the model fit's across approaches: R2a: 0.706 vs. 0.235. So far, my intuitive thinking is that small populations and rare persons cause massive variation in the observed per capita rate. E.g. in this dataset, the observed rate per million of top FIDE is ~100 in Faroe Islands and Iceland but only 9-11 in the rest of Scandinavia. Are we supposed to believe this reflects some real difference? Hardly. Secondly, this massive sampling error is not (apparently) completely counteracted by down-weighing the importance of small samples in the model, at least not using the sqrt approach. Perhaps one can develop a more suitable weight to use. However, using counts, it doesn't matter much if the count for a small country turns out to be 0 or 5 since a small number is predicted by the small population size in any event. For instance, Faroe Islands only has n = 5 (for population 50k), but it could have easily been 0 or 10 and neither value would have caused a major outlier using the counts approach, but would have done so using the per capita approach.
Why not use the non-log version? Theoretically, the use of logs should cause nonlinear interactions between IQ and population size to occur, but with n=200, we don't have a realistic chance to estimate these. I did try a model with the interaction, but we don't really have enough precision to estimate them either (bizarrely, it resulted in p = .006/.007 negative betas for IQ and population size, and the interaction with positive with p < .0001). Perhaps if one collected chess champions for some smaller unit, e.g. EU NUTS or USA counties.

