Personality structure problems

A review of the evidence for and against GFP (general factor of personality) and OCEAN (big five)

In hereditarian circles, there's a lot of talk about the general factor of personality (GFP). Briefly, the data shows that if you take typical Big Five (OCEAN) tests, they tend to be weakly correlated, even if they are supposed to be orthogonal by design. Because of these correlations, you will get a more general factor which has positive loadings on extroversion, agreeableness, conscientiousness, openness, and a negative loading on neuroticism (thus, it is sometimes called emotional stability (ES) and reversed). It sure sounds like there is a weak tendency for everything good to go together, even if we are usually told that personality dimensions do not measure something better or worse. Of course more neuroticism is bad. However, it is also true that personality dimensions of OCEAN have nonlinear valence. It is better to be low on neuroticism, but perhaps not being in the bottom 1st centile, as this means you are basically unable to have any worries, even when you should have them. The same for extroversion. Being very introverted is bad for your social skills, networking etc., but being top 1st centile probably means you spend all of your time hanging out with others, and no time doing some critical things that need to be done alone (filing taxes, reading), not to mention the drug abuse association. A review of these nonlinear findings of OCEAN traits is found in Five into one doesn't go: A critique of the general factor of personality (2011).

But let's get more numerical. It turns out that if you score people on the GFP and also on the general psychopathology factor of psychiatry, then these turn out to be much the same thing. Another way of saying this is that people with psychiatric diagnoses are usually highly neurotic, introverted, lazy and disorganized (low conscientiousness). This meta-analysis (Linking “big” personality traits to anxiety, depressive, and substance use disorders: A meta-analysis., 2010) shows many of these features:

So people with major depression (MD) are 1.33 standard deviations higher in neuroticism, a fact that probably doesn't surprise you. But they are also 0.90 d lower in conscientiousness. People with generalized anxiety disorder are 1.97 d higher in neuroticism, but also 1 d lower in extroversion, and 1.1 d lower in conscientiousness. Substance abuse diagnoses are lower in agreeableness by some 0.75 d. The results aren't entirely consistent, but clearly there are some strong correlations between psychiatric issues and personality traits from OCEAN models. Overall, diagnosis was associated with 1.65 d higher neuroticism, 0.90 lower extroversion, 1 d lower conscientiousness, 0.3 lower openness, and no association to agreeableness.

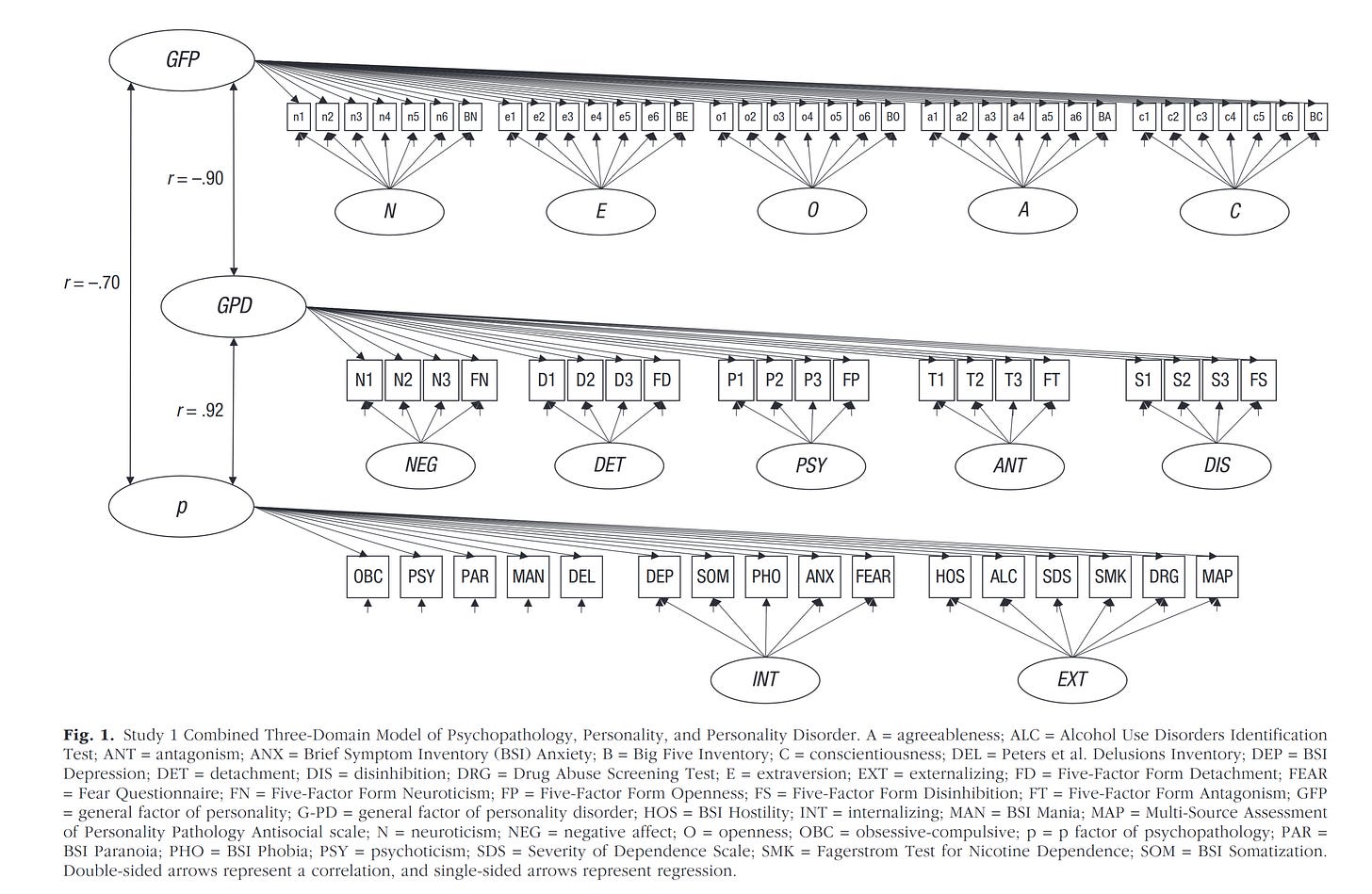
We could also just look at these general factors together, take this study (General Factors of Psychopathology, Personality, and Personality Disorder: Across Domain Comparisons, 2018):

There's a whopping -.70 correlation between the psychiatric general factor (P) and the GFP. This study also includes another variant that is in-between, the general factor of personality disorders. That one shows a -.90 correlation with GFP. These results aren't unusual, but have been replicated a number of times. Thus, it seems that the GFP theorists are right: there is such a thing as a good personality, overall, and we can clearly see this by comparison with psychiatric data.

We can go further yet. Many people like the emotional intelligence construct. Some of this is cope, as they don't like the big importance of regular general intelligence. But some of this is also real because most people are familiar with the socially awkward autist, Mensa member, who seems to achieve nothing in life despite 130+ IQ. It turns out that if you measure emotional intelligence using the standard tests, this also is much the same thing as the GFP (Overlap between the general factor of personality and emotional intelligence: A meta-analysis, 2017): "(a) a large overlap between the GFP and trait EI (r ≈ .85); and (b) a positive, but more moderate, correlation with ability EI (r ≈ .28)". For those not familiar with the emotional intelligence research, researchers have come up with two ways to assess this. As a personality trait, using the usual questionnaire format (trait EI), and as a kind of semi-objective test where people answer situational judgment-like questions (ability EI). The personality variant correlates .85 with GFP, so that's roughly the same thing. The ability variant doesn't correlate so much, but that's because it's probably mostly just regular intelligence, g-loading is about .80 (Emotional intelligence is a second-stratum factor of intelligence: Evidence from hierarchical and bifactor models. 2014).

And there's an assortment of other findings:

• GFP correlates with physical attractiveness ("Both self-rated (β = .14, p < .001) and rater-based (β = .12, p < .001)")

• GFP correlates with job performance (about r = .23)

• GFP correlates with self-esteem (rather highly)

• GFP correlates with peer-rated likeability and popularity

• and so on, you can read the reviews from the pro-GFP camp, mainly represented by Dimitri van den Linden and Janek Musek

Anti-GFP findings

So far so good, but there are some critics too. Take this paper by eminent psychometrician Bill Revelle and his colleague Joshua Wilt (The General Factor of Personality: A General Critique, 2013):

Recently, it has been proposed that all non-cognitive measures of personality share a general factor of personality. A problem with many of these studies is a lack of clarity in defining a general factor. In this paper we address the multiple ways in which a general factor has been identified and argue that many of these approaches find factors that are not in fact general. Through the use of artificial examples, we show that a general factor is not:

1. The first factor or component of a correlation or covariance matrix.

2. The first factor resulting from a bifactor rotation or biquartimin transformation

3. Necessarily the result of a confirmatory factor analysis forcing a bifactor solution

We consider how the definition of what constitutes a general factor can lead to confusion, and we will demonstrate alternative ways of estimating the general factor saturation that are more appropriate.

They present a number of arguments, but the main one in my opinion is that the GFP is rather weak. Here's some results in comparison with the well known general factor of intelligence (every other construct in psychometrics wants to be as solid as g):

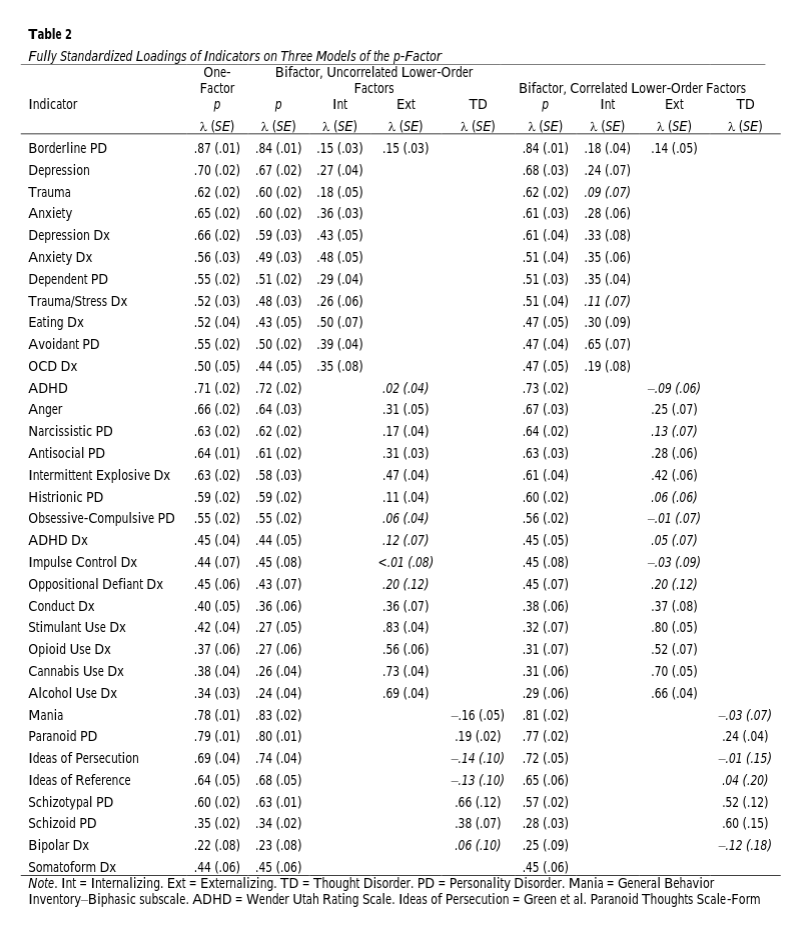
The different columns are different metrics for measuring how strong a general factor is. The most psychometrically appropriate is probably the omega hierarchical. We see that this value is about .80 for intelligence (g), but only .48 for GFP. So the GFP is much weaker. This is a different way of saying that the general factor loadings of the OCEAN traits is usually only .30 to .40, while a good intelligence test will be up to .80. An intelligence test with only a g-loading of .40 would be considered poor. OK, but one could say that this is just due to the inherent harder difficulty of measuring the GFP. Perhaps! If we look at factor loadings on the general factor of psychopathology, we do see that the factor loadings are sometimes quite high (Defining the p-Factor: An Empirical Test of Five Leading Theories, 2022):

In this study, borderline personality has a p-loading of .87. Readers familiar with such people will probably agree with this. But many others are also quite high, e.g. manic personality (.78), ADHD .71. But quite a number of the others are not very high, say, cannabis addiction .38, or eating disorders .52.

In a detailed study using both self and peer reports of personality (Construct validation using multitrait-multimethod-twin data: The case of a general factor of personality 2010), one can sort of squeeze a GFP (as well as the alpha/beta AKA stability/plasticity) out of the OCEAN data, but they have quite weak loadings: "However, the GFP explained only 6% (E) to 11% (A) of variance in the Big Five. Consequently, just about 2% (self-report ES) to 6% (peer-report A) of variance in the manifest variables was accounted for by the GFP.". In terms of factor loadings, then, the average item loading on GFP would be about .20. This is generally considered to be very poor. The family dataset used in the study wasn't quite large enough to really tell the models apart using model fits, so we will have to wait until someone finds a bigger dataset for this. Overall, the GFP is a very weak factor compared to the usual factors in psychometrics, but whatever it is, it does correlate with a bunch of positive stuff (listed above). The question is what that means. It's not like the GFP has any validity beyond the OCEAN -- it's a linear composite of them so that's impossible -- but whether it's a useful way of looking at things.

Predictive validity

Another way to look at this is to ask whether we can predict outcomes in life better using a general factor, OCEAN factors, OCEAN facets, or individual personality items. If the validity of personality is in the general factor, then using lower order constructs will not markedly improve the validity. This is the pattern one sees for intelligence, where the g factor contributes the largest share of the validity (see prior post on principal component regression and g). Again, we have to thank Bill Revelle, David Condon and coauthors for looking into this (Leveraging a more nuanced view of personality: Narrow characteristics predict and explain variance in life outcomes, 2017):

Among the main topics of individual differences research is the associations of personality traits with life outcomes. Relying on recent advances of personality conceptualizations and drawing parallels with genetics, we propose that representing these associations with individual questionnaire items (markers of personality “nuances”) can provide incremental value for predicting and explaining them—often even without further data collection. For illustration, we show that item-based models trained to predict ten outcomes out-predicted models based on Five-Factor Model (FFM) domains or facets in independent participants, with median proportions of explained variance being 9.7% (item-based models), 4.2% (domain-based models) and 5.9% (facet-based models). This was not due to item-outcome overlap. Instead, personality-outcome associations are often driven by dozens of specific characteristics, nuances. Outlining item-level correlations helps to better understand why personality is linked with particular outcomes and opens entirely new research avenues—at almost no additional cost.

Thus, if you want to predict outcomes (10 different ones analyzed here), then it is best to predict from items, not from OCEAN, or from facets:

Say, you want to predict educational attainment. You can use the OCEAN, and you get an R2 of 6.7%. But if you use the facets, you get 16.7%, and if you use items, you get 26.6%. In correlations, these are .26, .41, and .52. So using items is about twice as good as using the popular OCEAN scales. There isn't any GFP in this study, but it's value would at most be the same as that for OCEAN, and in practice will be even smaller. In other words, we might say that personality is generally more important than is thought because psychologists aggregate their data too much in order to make predictions. On the other hand, these item-based predictions are not very interpretable. In other words, what we have is a trade-off between interpretability and predictive validity. This trade-off is very familiar to those working in machine learning. Deep neural networks are basically uninterpretable black boxes, and they attain the best predictive validity, and can build us amazing AI agents.

One thing that bothers me about the item-level approach is that many items are things like "I tend to overeat", which unsurprisingly is a good predictor of BMI, but we aren't too surprised that food impulse control, a pretty specific character aspect, predicts BMI. Here's the top 10 items for each outcome:

Looking at the list of item-level BMI correlates suggests to us that Geoffrey Miller was on to something in his infamous tweet:

Which personality structure?

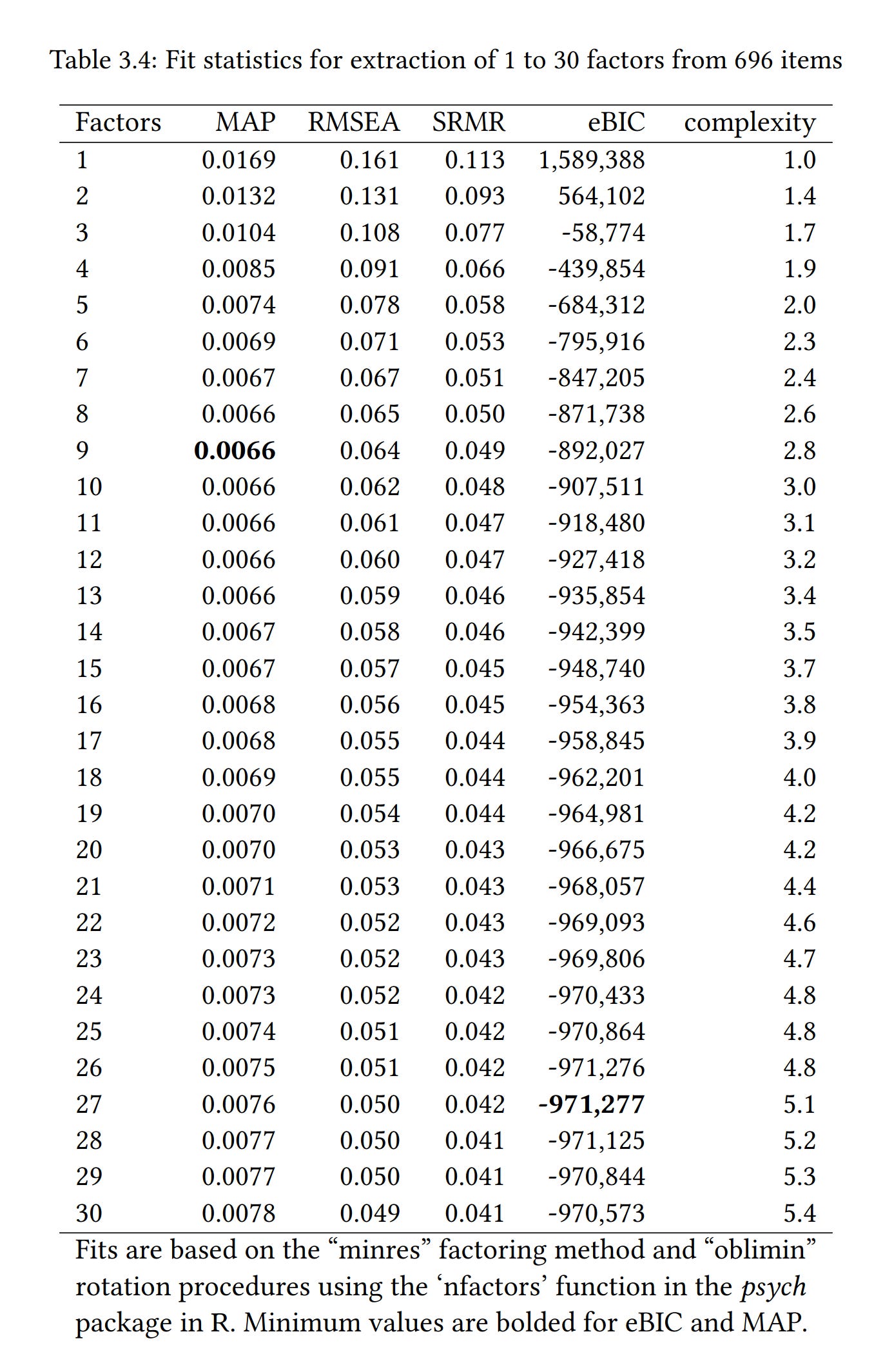
In light of such findings, we might also ask: is OCEAN really the right level of aggregation in general? Maybe the HEXACO people are right, or the alternative Big Five people. One way to look at this question is to take a very large pool of items, and apply some statistics to figure out the 'best' statistical model. Again, Bill Revelle has been on point. His former student David Condon have done this already (An organizational framework for the psychological individual differences: Integrating the affective, cognitive, and conative domains, 2014, PHD thesis):

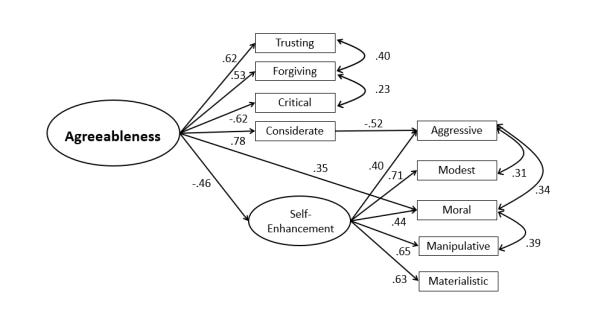
In this case, Condon used 4 different "goodness of fit" metrics, or number of factors to extract methods. Unfortunately, two of these indicated that more is always better (RMSEA, SRMR), MAP said 9, and eBIC said 27. None of these numbers are "5" to be sure, and they don't agree with each other either. Optimistically, we could conclude that these metrics aren't all suitable for this question. Or maybe we should conclude that there isn't any correct or optimal level of aggregation of personality in general. This result has been replicated with a different sample of some 104 agreeableness items from various personality inventories (The Structure of Agreeableness, 2020):

So 3 methods wanted 20 factors just to explain agreeableness subdistinctions (!), another wanted 12, and the last 16. What are we to make of this? Schimmack himself decides to try some theoretical models and comes up with this model:

The model fit is fine, but if we had taken some other collection of items, would we really expect this to replicate? I don't think so. Personality structure is very complicated.

A final way to look at the hierarchicalness of personality is to carry out successive factor analyses starting with 1, then 2, then 3, etc. factors. The predictions from a hierarchical model is that factors will tend to split across hierarchies, in the same way we can split the g-factor of intelligence into VPR (or whatever), and these furthermore into fluid reasoning, short term vs. long term memory and so on. The eminent behavioral geneticist and psychometrician John Loehlin tried this approach before and got this result:

Are personality traits mostly related to one another in hierarchical fashion, or as a simple list? Does extracting an additional personality factor in a factor analysis tend to subdivide an existing factor, or does it just add a new one? Goldberg’s “bass-ackwards” method was used to address this question, based on rotations of 1 to 12 factors. Two sets of data were employed: ratings by 320 undergraduates using 435 personality-descriptive adjectives, and 512 Oregon community members’ responses to 184 scales from 8 personality inventories. In both, the view was supported that personality trait structure tends not to be strongly hierarchical: allowing an additional dimension usually resulted in a new substantive dimension rather than in the splitting of an old one, and once traits emerged they tended to persist.

We don't generally see much splitting as we force the model to extract another dimension from the items. It looks like the models just keep adding more dimensions.

Conclusions

We could keep going with more difficult-to-integrate findings, but:

• Most psychology aggregates personality data to 5 dimensions, the familiar OCEAN. This is based on Galton's initial ideas about taking every adjective in a dictionary and analyzing them (lexical hypothesis).

• Model fit statistics on large datasets of items don't really support this 5 factor solution, nor do they support any other number in particular. Unsatisfying.

• In fact, modeling of personality data in general do not suggest they are hierarchical to a strong extent.

• Predictive modeling shows that using items -- the most possible dimensions -- is best for prediction by a wide margin.

• But data also shows that one can sort of extract a general factor of personality -- the least possible number of dimensions -- and this has fantastically strong correlations with psychiatric problems and the general factor of these in particular, thus enabling one to talk about a general "good personality" and a bad one.

• Do we have to accept the unsatisfactory conclusion that there isn't any particularly globally optimal structure of personality, but that this depends on what you want to do with the data (predict vs. understand vs. psychiatry)?

• Major caveat: most data analyzed here are based on self-report, which could induce systematic distortions. A few are based on peer-report data, which mostly produced congruent results. One can use word embedding as a kinda weird alternative, and for that, see the Vectors of Mind blog.

• I don't really know what to make of this in general. It's a big mess.

I asked Bill Revelle what he thought of this, and he said (among other things):

I remain a sceptic of the GFP as well as the p factor of psychopathology. You might enjoy the talk I gave at ISSID suggesting that we should not over interpret factor structures. (https://personality-project.org/sapa/issid.pdf) Factors are merely convenient fictions to allow us to summarize covariance matrices.

David Condon adds more recent work to check out:

You may find my slides from a recent talk about some of these topics useful: tinyurl.com/BigFiveARP2023

Also, I think the SPI paper is more aligned with your arguments than my dissertation (but thank you for even being aware of it). See here: https://psyarxiv.com/sc4p9/
The Cutler and Condon paper that Bill mentioned is now in press here. I'm glad to see that you linked to his blog too.