What do genomic principal components mean?

The first sibling admixture study

There's a new study out making the rounds, but first I want to divert and ask: Who invented admixture regression? Here I mean the analysis where admixture (ancestry) estimates of individuals are used to predict their phenotypes. These ancestry estimates can be given as proportions of some 'purebred' populations, as is typically done on 23andme and other consumer genomics platforms. It turns out, the answer is not Arthur Jensen, though he was an early proponent of using this method to clarify causality for race and intelligence. It was William Shockley. He published a relatively unknown paper in Science journal (that's a big name journal) in 1966:

• Shockley, W. (1966, January). Possible transfer of metallurgical and astronomical approaches to problem of environment versus ethnic heredity. In Science (Vol. 154, No. 3747, p. 428).

Notably, this was before Arthur Jensen's famous 1969 article that started the modern debate. In fact, the entire Shockley paper is only this long:

The analogy proposed here makes impure "chemically pure" elemental metals correspond to impure "genetically pure" populations and makes a radioactive tracer atom correspond to a tracer gene G_i - for example, blood type or taste discrimination-that occurs in different fractions a_i and b_i of individuals in "elemental populations' P_A and P_B. A large group of G's can be used to measure, for each individual studied (rather than for populations), the "ethnic composition fractions" f_A and f_B of the individual's genes that come from P_A and P_B ancestors. Measurements of f become potentially highly reliable as advances in biochemistry and genetics identify additional G's. A proposed ethnic composition index is

where 8_i = 1 or O if the individual has or has not G_i and the sum extends over all identifiable traits. For random G selections, expected values of H vary from +1 for pure P_A to -1 for pure P_B or generally equal 2f_A - 1. (H should be modified for correlated G's. ) That the expectation value of an individual's performance is independent of ethnic composition (that is, ethnic heredity is trivial compared with environment) should be possible to establish or to reject to a high level of statistical significance by observations on siblings of mixed P_A-P_B ancestry. Data about such individuals, whose prior development is uninfluenced-by the study, are analogous to data of pre-sputnik astronomy. Like selected sequences of stars, siblings provide one controlled variable (same family home environment) and one observable varying feature (values of H should differ significantly for siblings, especially for offspring of first generation P_A-P_B hybrids). For example, correlation of physical, mental, and social measurements with one another and with values of H might give scientific support for Washburn's proposal (that is, for equal environments American Negroes might surpass whites) by showing a positive correlation of performance with fraction of Negro genes. Data on correlations of G's would be genetically significant and relevant to I.Q. and other polygenic traits.

So in just a few words, he invents the first individual-level admixture estimator (never used as far as I know), and even proposes a sibling control study to clarify Black-White IQ gap. Some of his later writings speculate further on this. For more about this history, see this post.

That brings up to modern times. Here's the paper everybody is talking about:

• Sotoudeh, R., Trejo, S., Harpak, A., & Conley, D. (2024). Does standard adjustment for genomic population structure capture direct genetic effects?. bioRxiv, 2024-05.

Contemporary genomic studies of complex traits, such as genome-wide association studies (GWASs) and polygenic index (PGI) analyses, often use the principal components of the genotype matrix (PCs) to adjust for population stratification. In this paper, we explore the extent to which we may be discounting direct genetic effects by adjusting for PCs. Using family-based models that control for parental genotype (obtained via Mendelian imputation), we test whether PCs have a direct genetic effect on nine complex phenotypes in the White British subsample of the UK Biobank. Further, we assess the extent to which estimates of polygenic effects meaningfully change when adjusting for PCs in within-family models. Across the nine traits, within-family effects of the top 40 PCs are highly similar to their population effects, suggesting that standard PC adjustments diminish, albeit to a small degree, detectable signals of direct genetic effects. Within family models also confirm that PCs have significant marginal effects on a few traits, most consistently, height and educational attainment. Nonetheless, the variance explained by the effects of PCs is modest, and adjusting for PCs does not appear to affect the magnitude and significance of PGI effects in within-family models.

If you have been reading debates about genomics of race, polygenic scores etc. you will know that criticizing a study for not sufficiently controlling for 'population stratification' is a kind of mantra among egalitarians. This new study shows that this is not so easy because the principal components may have some causal signal in them, so controlling them removes part of the signal. Mathematically, principal components are merely the best way to describe a typically larger number of variables by positing unseen (latent) dimensions (variables) in the data, formed by adding up the original (observed) variables using the right weights (loadings). Principal component 1 (PC1) is the one that explains the most variation in the original variables, PC2 the next-most, and so on. The PCs are themselves uncorrelated by design. As such, principal component analysis is thus about the same as running a factor analysis with orthogonal (uncorrelated) factors. (Some purists will complain about this conflation because the math of principal component analysis is very different from factor analysis, but the results are usually about the same.)

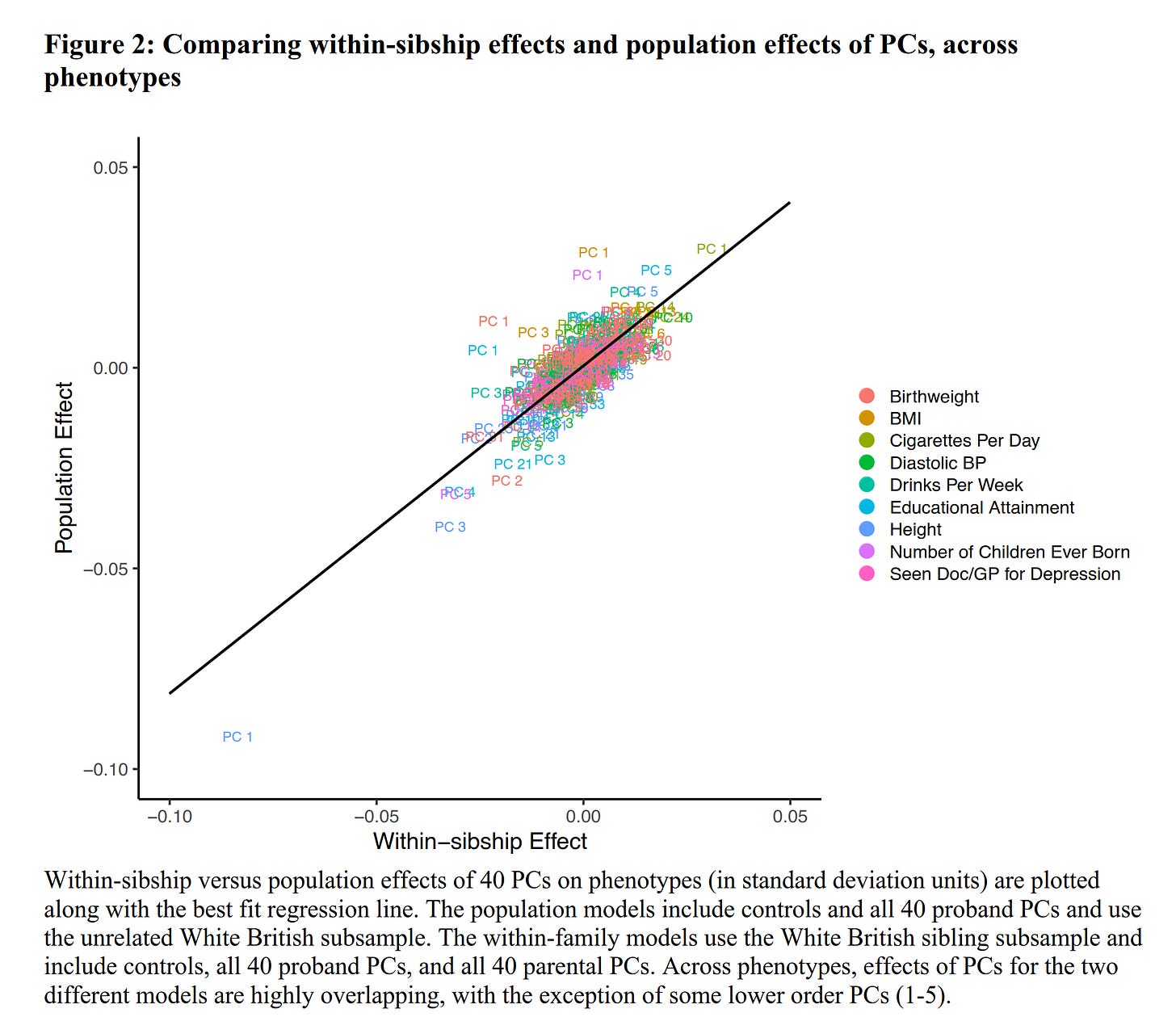
In their new study, they train a model to extract PCs on British Whites in the UK Biobank, and then use the sibling and full samples to see if these PCs predict phenotypes. They find that they do:

Given the noise, they aggregated the results across a number of phenotypes, notably including educational attainment. Overall, they show that the effects of these PCs are about the same within and between families, same direction and roughly same effect size. Thus, we know that the PCs capture something aside from mere 'population stratification' taken to mean unseen environmental variables that cause differences between subjects that relate to ancestry, including intra-British ancestry. Because of these probably causal effects of ancestry, one cannot just control for them in a regression model without making causal assumptions. In fact, by not controlling for PCs, one would be maybe under-controlling for unseen environmental effects, but by controlling for them, one would be over-controlling for some of the true genetic effects. There is no perfect solution -- both approaches have some bias -- at least if one is using PCs as the approach.

This figure shows the effects of the first 8 such PCs across their 9 chosen phenotypes. Interestingly, we see that PC1 predicts height negatively. What is PC1? They unfortunately don't provide us with a map so we can see where these components are low and high, but they do provide this figure in their supplements:

We see that PC1 thus reflects latitude and PC2 reflects longitude (higher = west). The components analysis isn't being told to find geography, it just falls out of the data naturally, though rotated. It's rotated because PC1 must explain the most variation and it unsurprisingly turns out north-south is more important in England than east-west. This is typical for the first 2 PCs, which usually represent geography.

When their study thus finds that PC1 predicts height negatively, what they have shown is that even among siblings northern, Scottish ancestry predicts lower height. It's the first sibling admixture study akin to what Shockley proposed, though slightly cryptically done. Similarly, their PC2 predicts height negatively, and we know this represents Welsh ancestry, so the Welsh are also shorter than the English genetically speaking. There may also be differences among the English themselves, because we know that the admixture of the British people has a geographical gradient so that the Germanic ancestry proportion is larger in the south.

CNE = continental northern Europeans (Dutch-German-Danish), IA = Iron age.

The English have a large admixture components from the Germanics (who are similar to French iron age samples), whereas the Welsh and Scottish don't have so much of this.

Their study also found effects of later PCs on educational attainment. However, the only reliable signal was that PC4 and PC5 predict educational attainment negatively and positively. But since we don't know what these PCs mean in ancestry terms, we can't really interpret them. They could represent other old admixture, say, Huguenot elite migrants from France. Maybe someone else can re-do their PCA and show some maps so we can figure out what PC4 and PC5 mean.

This new paper follows a similar one from 2020 which made the same theoretical points regarding principal component controls being problematic. So I would say in general, there's progress among the mainstream geneticists in coming to terms with race differences. Now we just need them to repeat this analysis with siblings from all ancestries, not merely the British. The trouble with this is that siblings are rare in datasets, so perhaps no single dataset has the thousands of sibling pairs needed to do this with statistical precision (even this study is underpowered, as seen in the confidence intervals above). However, maybe it can be done using pooled datasets. Since the collection of genomic datasets is only gathering speed, in the next few years there should be more datasets with sufficient data.