On having negative knowledge

Are some voters systematically misinformed about basic political facts?

I'm reading Jason Brennan's 2016 book Against Democracy, actually in favor of votes weighted by competence, which he calls epistocracy. In discussing the very low levels of political knowledge seen in surveys, he writes:

Ignorance is not uniform. As Converse says, while the mean level of knowledge is low, variance is high. Most voters are ignorant, but some are highly informed, and some are worse than ignorant.

The ANES surveys eligible voters on basic political information, such as who the candidates are or what these candidates stand for. There is tremendous variance in what eligible voters know. Political scientist Scott Althaus summarizes some of the results:

Just how high [the variance is] is made clear when we add up the number of correct answers to these questions and divide respondents into knowledge quartiles. While people in the highest knowledge quartile averaged 15.6 correct answers out of 18 possible, people in the lowest averaged only 2.5 correct answers.³⁸

On this test of political knowledge, the top 25 percent of voters are well informed, the next 25 percent are badly informed, the next 25 percent are know-nothings, and the bottom 25 percent are systematically misinformed.

The ANES in effect gives citizens a multiple-choice exam on basic political knowledge. As we saw above, the voting public as a whole does worse than chance on many of these questions. In the 2000 US presidential election, significantly less than half of all Americans knew that Gore was more supportive of abortion rights, more supportive of welfare state programs, favored a higher degree of aid to blacks, or was more supportive of environmental regulation that Bush. Think of what that means. Imagine you are on Who Wants to Be a Millionaire. The host asks you the million-dollar question, “Who was more supportive of abortion rights in 2000, Al Gore or George Bush?” Suppose you don’t know, but the host gives you the option of either flipping a coin or phoning a random US voter from the year 2000. You should flip the coin; it’s more reliable.

There is a claim that the bottom 25% of subjects are not merely ignorant, but misinformed. They know less than would be expected by chance; call it negative knowledge. But this conclusion is mistaken. I will demonstrate that using simulations:

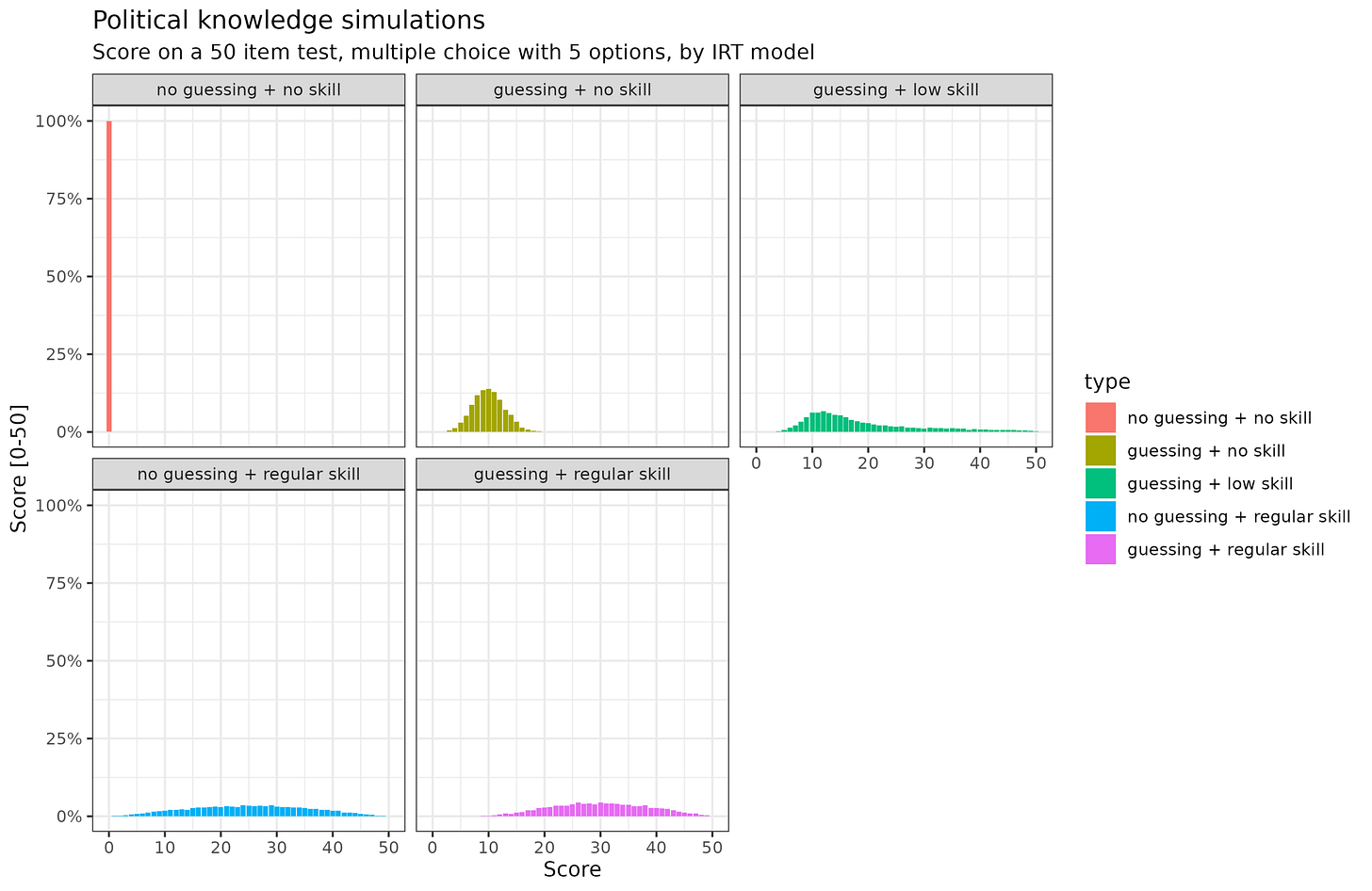
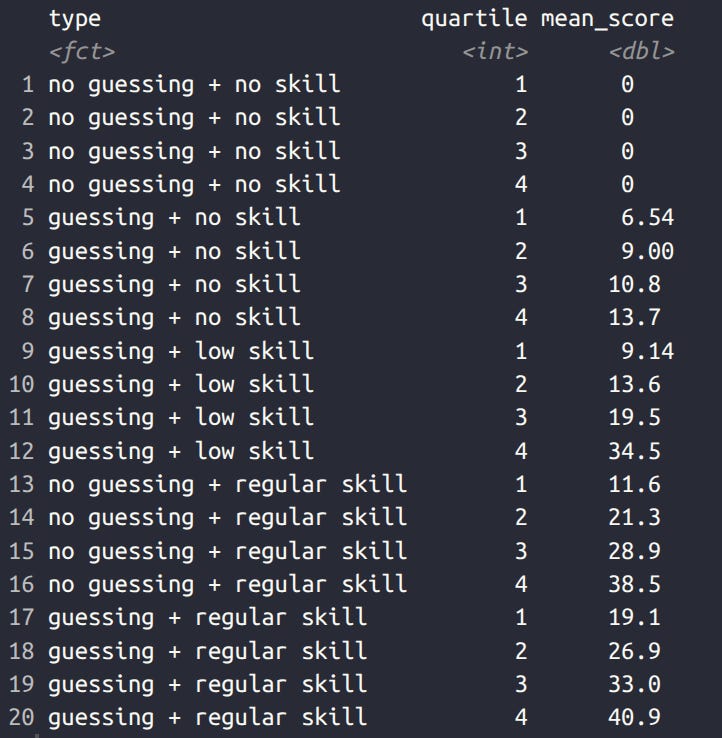
Consider a fairly typical 50-item (question) knowledge test. How can we model the data? Well, we can consider a test where people cannot guess the answer if they don't know (open-ended responding). This is not so realistic (maybe someone will write George Washington to every question and get 1 question correct), but is hypothetically possible. If we have a sample of subjects of very low knowledge level, their score on the test will be 0 (in red, 2PL model). However, if we consider a more typical scenario where each item has 5 options, then subjects have 20% (1/5) chance of getting it right by (blind) chance. Thus, the score mean will be 10 (50*1/5) with some variation above and below depending on how lucky the subjects were (in yellow, 3PL model). We might also consider the situation where some subjects have some but not much knowledge, in which case they will perform a bit above chance (in green). Finally, we might consider a test properly made for these subjects' knowledge-level with and without guessing (blue and purple). Reality is somewhere in between low and moderate skill (green and purple), and this means that some subjects will perform at below-chance levels purely due to being unlucky guessers and having little knowledge. This result does not show that they are systematically misinformed. Here's the quartile averages by scenario:

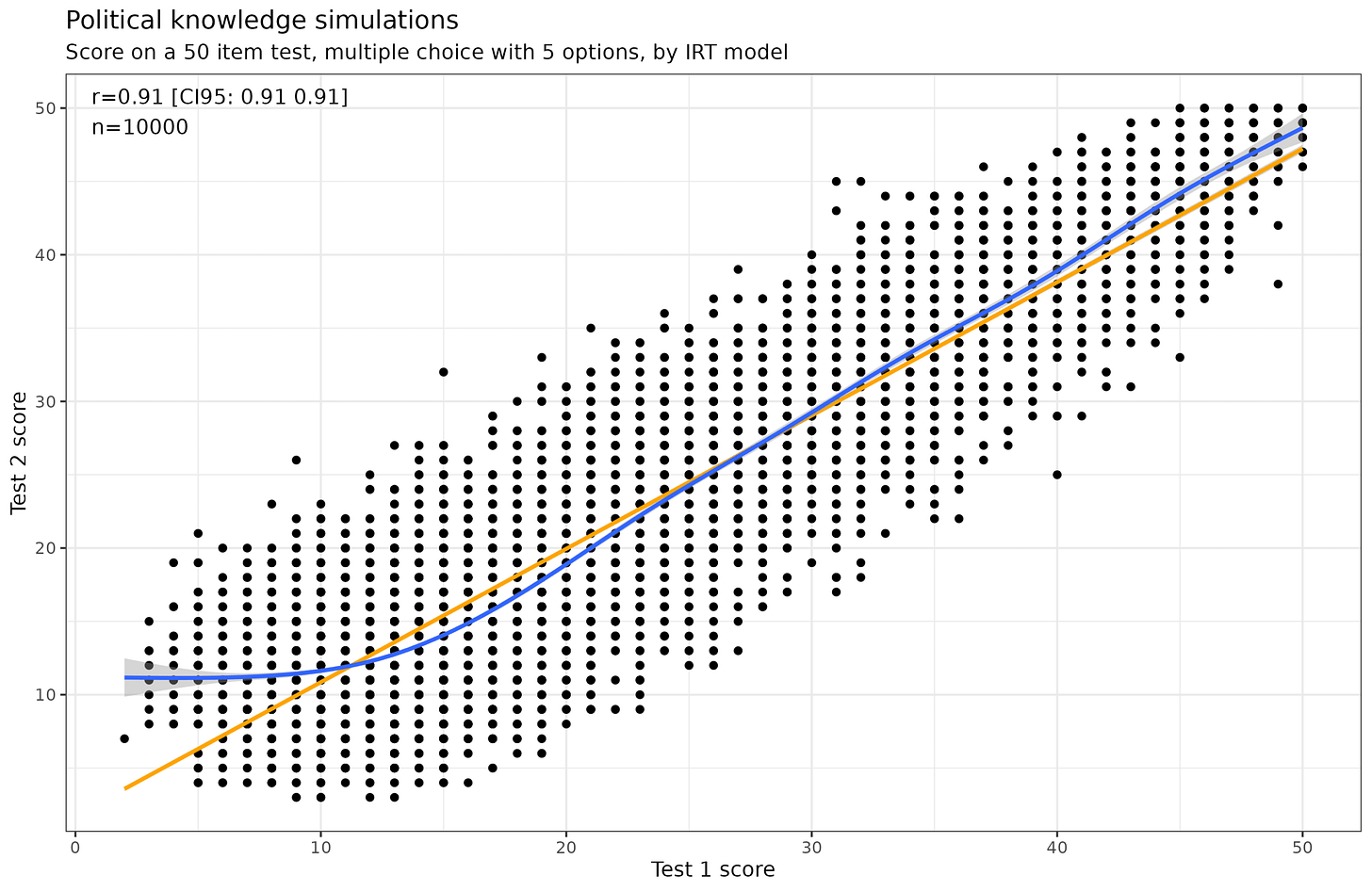
For the situation with low skill + guessing, we see that the average score of the 25th centile is below 10, that is, below what one would achieve by chance alone. However, none of these simulated subjects were systematically misinformed, they were merely ignorant and unlucky. The real test of Brennan's model is that when subjects are given two tests on different occasionally about different pieces of knowledge, those below guessing level on the first testing will also be below-chance on the second testing. Some of them may be, but that is also expected by chance. Given their initial low skill level, the is there be about 50% chance for these to be below guessing level again. A smoothing regression model will thus show no slope below the guessing chance score:

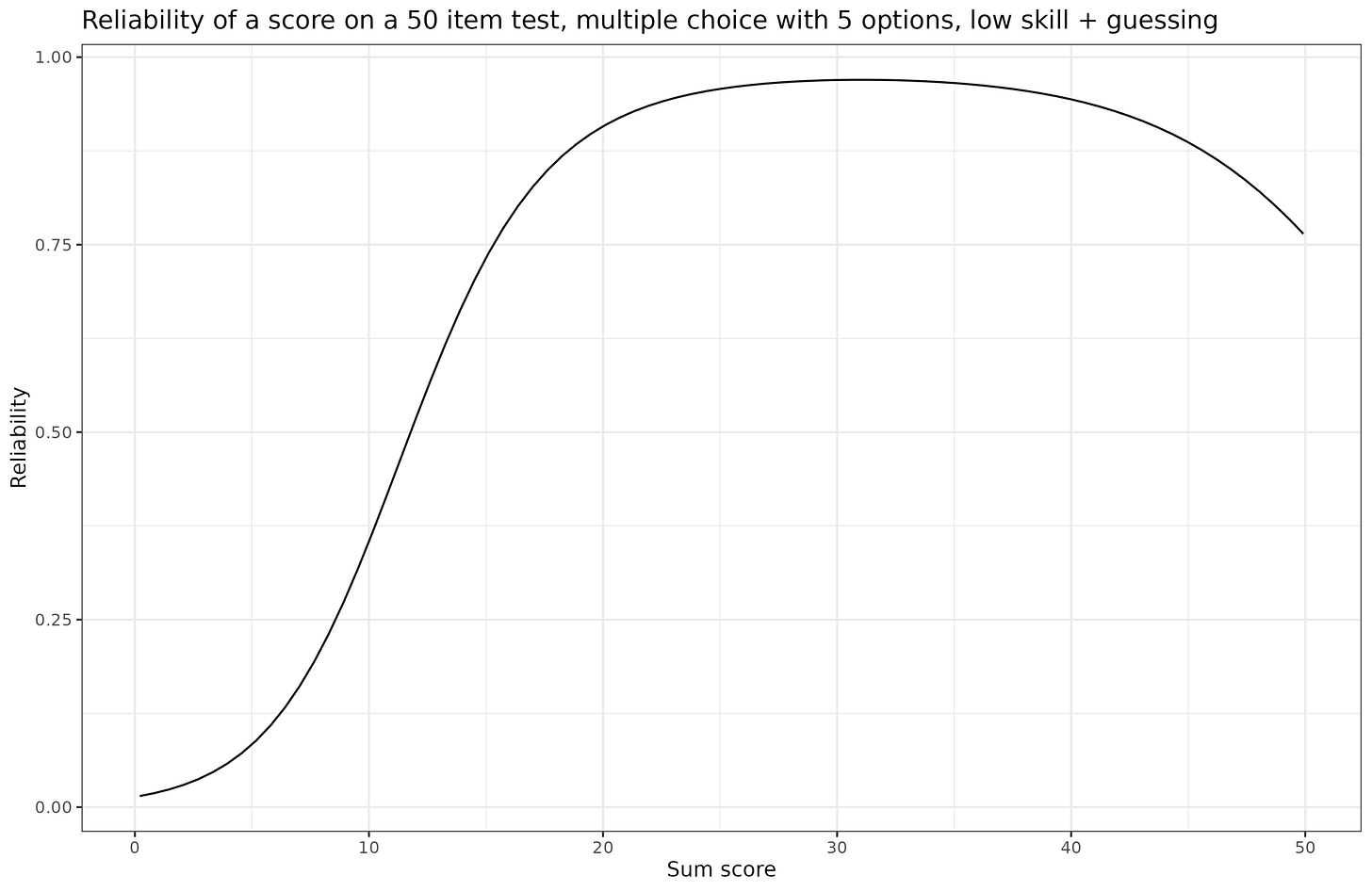
Which is what we do in fact see in the simulation. Another way to approach this is to look at the reliability as a function of skill level:

And we see as expected that the reliability of the score declines to near-0 once we get close to random guessing. After all, random guessing is by definition not correlated with anything, including itself on a second occasion.

Finally, this is all very hypothetical. Do we have some real results for this? Best would be to conduct such two surveys, or split one longer survey into two parts. However, since we can also calculate reliabilities by subgroups as a function of their test score, that method is easier. This has sort of been done in a twin study concerning political opinions by looking at the heritability results:

The E component in classical twin models (ACE) concerns any source of variation between subjects that makes them different from one another, but is not related to upbringing or genetics. This is mostly noise (not something one can manipulate; gloomy prospect), including random measurement error. Thus, unreliable measures will produce higher E%, and lower A% and C% values. Looking at the values in the table above, we see indeed that the E component increases starkly in size when looking at less informed subjects. The assumption needed to interpret this study is that when subjects are low in knowledge on the 5-item knowledge quiz, their political opinions will also be fairly random.

I looked in the literature for someone pointing out this issue or doing a proper evaluation of misinformedness, but didn't find anything in a quick search. Readers can perhaps find something.